bullet above bore's axis...?

A quick clarification - Nothing I see in the math suggests the bullet rides the wind in a continued yawed position and with continuous lift effect. It seems the vertical seen at the target is a result of that overturning moment and brief period of instability while making the correction into the changing airflow.

If I am in error by all means please call me out. I'm always willing to learn.
 
Gene Beggs said:
Joe Woosman said:
… "The Rest Of The Story" ...
Click to expand...

Thanks for the story, Gene. It made me go out to the shop and do the Dremel test - an excellent way to visualize what happens to a bullet! A wind from right to left pushes on the center of pressure, which is forward of the center of gravity. This tends to turn the nose of the bullet to the left, but the gyroscopic reaction is that the nose of the bullet rises. This is confirmed by the Dremel tool test. The direction of reaction is defined by the right hand rule (See the attached sketch). Point your index finger in the direction of bullet travel from a right hand twist barrel. The direction of spin is counterclockwise looking from your extended finder back toward your hand (the origin of the coordinate system). Point your palm upward such that the moment that the wind creates around the CG of the bullet is also counterclockwise around a vertical axis. (You will have to imagine the sketched hand tilted 90 degrees. Sorry, it was the best I could find without drawing it myself.) Now the precession reaction will be counterclockwise around your extended thumb, again looking from your thumb back toward your hand, which results in the nose of the bullet rising.

The next step is to think about a bullet traveling nose high. It has a wind force applied to it that wants to push the nose even higher. But the gyroscopic reaction is such that the bullet nose now turns right. This reaction is also explained by the right hand rule. What I have described are two instants of the continuous process of precession - each time the nose is pushed in a changing direction, the orthogonal reaction direction changes also.

If the bullet is stable, then the precession angle decreases with each turn until the bullet faces into the vector resultant of its velocity and the cross wind velocity. But the bullet's velocity is not constant. It slows down, causing the constant cross wind velocity to be larger by comparison. This increasing relative cross wind causes more precession, the same as described above. Throughout its precession cycles, the bullet nose is, on average, angled to the left and upward, which causes the deflection that we see on target.

right hand rule.jpg
Click to expand...
 
First a few facts: Right hand twist always gain to the right from the view of the wind. Secondly increasing twist rate always increases the angle represented by the gain. So what am I talking about. I too am a former pilot so I have seen these effects at some rather high speeds. when you throw a top on the ground it will helix to the right, gaining position from its center in the direction of the spin. If the top is off center it will have a larger diameter to the helix and if it is spinning pure it will have a smaller diameter. But it will always gains to the right. If you think about the bullet the same way and envision a clock where you always have the wind directly to your back, the bullet will hit in front of you and to the right - always. When the wind comes from 3 o'clock it strikes left and high (right from that view) from 6 o'clock the bullet strikes in front of you and right of center, and when the wind comes from the (left) 9 O'clock to strikes in front of you and right (down ). In other words the bullet in reacting to the relative wind the same way each time viewed from the direction of that wind. It will always flow down wind and to the right, how much right is determined by twist, stability and wind speed. As I remember ( do not take that to the bank) my GS numbers a 13.5 twist bullet will gain 17 degrees on the right of the wind line. In order for you to see what I am talking about think of yourself on a clock face with the wind to your back.
 
WOW !! Two thumbs up for Joe Woosman !!

Joe Woosman said:
Thanks for the follow-up Gene.

Over the Thanksgiving festivities the last few days I've been giving this a lot of thought. I had to go back and do some studying to try and find the error in my thinking. I THINK I've got it corrected now but I must admit I have to rely a LOT on the work of others, particularly in the math department. The Ruprecht Nennstiel "How Bullets Fly" page is the most comprehensive and easy to absorb work I have found so far.

With a right hand wind/right hand twist, the bullet nose up and yawed to the right explains the effects seen on the target. A gyroscopically stable bullet must correct course into the wind or it would not be stable. If it pointed nose down we would not see what we do on the target. This is why it was so disturbing doing your Dremel test. Indeed if you turn the Dremel to the right in dives nose down!

After reviewing my materials, I believe the bullet really does end up exactly as I stated, (nose up and to the right), but how it got there was not covered. The math says a wind force from the side applies its force to the center of pressure. The center of pressure on a typical bullet is forward of the center of gravity, (closer to the point of the bullet). This force applied at the center of pressure turns the nose of the bullet about its center of gravity. So if you hold a bullet, or your Dremel, in the center and apply a force from the right near the point of the bullet or the cutter on the Dremel, it turns to the left!!

The gyroscopic forces then resists this change causing a yaw motion up. This is easily felt with your Dremel test. The bullet nose begins to oscillate in a conning motion until it becomes gyroscopically stable again pointing into the direction of airflow. This is called the overturning moment.

Many years ago I studied this stuff and I did have this understanding. I believe the motion between stable in no wind and stable in right wind was lost in the DMA (doesn't matter anyway) of bullet flight. Just accepting the nose up and to the right explains what is seen on the target.

I would add this, the lost motion probably helps explain what Landy observed in his test where there was a greater wind effect where the bullets entered the wind.

Good stuff!
Click to expand...




Joe Woosman, I congratulate and thank you from the bottom of my heart for the best explanation I have ever heard of how gyroscopic force causes the left/up phenomena we see on the target when shooting in a right to left crosswind!! :D:D:D FANTASTIC MY FRIEND! :eek: :D

At last, someone has finally filled in the missing pieces of the puzzle I've been trying to resolve for years! :D Thank you, thank you thank you! :)

Yes sir, Joe it's obvious you have given this a lot of thought. It is also obvious that you are a very smart man with the ability to model complex, 3-D parts and movements in your mind's eye. You are also a terrific writer. We are so fortunate to have you back with us on Benchrest Central. I look forward to meeting you.

Sincerely

Gene Beggs
 
No

Alaninga said:
It would take a crosswind from the LEFT to cause bullet to rise, same right twist bullet.
Left wind effect: bullet goes UP and RIGHT.
Wind from right: bullet goes left and down.
Click to expand...



Alaninga

I'm sorry but you are mistaken about this. What you stated above is exactly backwards from what really happens. Do a little studying and if you don't get squared away get back to me and I'll help you. :)

Gene Beggs
 
Good point !

expiper said:
I usually shoot a sighter and see where it goes,,,Roger
Click to expand...



Now there's a common sense solution. :)

Almost without exception, the best way is always the simplest, easiest way.

We OCD types are bad about over complicating things but that's just our nature. We want to understand what happens to the Nth degree. Does it help our shooting? Nah, no way. :rolleyes: If anything it probably hurts our competition shooting. :p

Later,

Gene Beggs
 
Joe Woosman said:
A quick clarification - Nothing I see in the math suggests the bullet rides the wind in a continued yawed position and with continuous lift effect. It seems the vertical seen at the target is a result of that overturning moment and brief period of instability while making the correction into the changing airflow.

If I am in error by all means please call me out. I'm always willing to learn.
Click to expand...

Joe,
It's not a brief period of instability or "jump" as some have called it. An overturning moment keeps appearing as the velocity of the bullet slows down. This changes the direction of the resultant wind, thus precession and deflection is continuously driven from the muzzle to the target.

Cheers,
Keith
 
mks Thanks for the story said:
15590[/ATTACH]
Click to expand...



Hi Keith, thanks for joining the conversation. It's always nice to get your input on things although a PHD such as yourself often describes things in ways that are hard for an uneducated redneck like me to understand. :rolleyes: I will have to study your response for a while until it becomes clear what you're saying. I'm sure you're right as I've never known you to be mistaken about anything and I'm not being facetious when I say that; it's simply the truth. :eek:

I'll close and lock the door to the computer room before doing the finger gymnastics you suggested so no one will think I've gone completely mad. :eek:

Oh how simple and wonderful life was when I was a kid. If I wanted to go shooting I just grabbed the old Marlin 22, a box of shells and off I went to plink or hunt jackrabbits. Yep, those were the days.

Since getting into benchrest group shooting in 1987 or thereabouts, the more I learn about extreme rifle accuracy, the more I realize just how much more there is to learn. :rolleyes: But it's fascinating and fun; huh?

I'll get back to you later after I study a bit.


Best regards

Gene Beggs
 
mks said:
Joe,
It's not a brief period of instability or "jump" as some have called it. An overturning moment keeps appearing as the velocity of the bullet slows down. This changes the direction of the resultant wind, thus precession and deflection is continuously driven from the muzzle to the target.

Cheers,
Keith
Click to expand...

Keith,

I both agree and disagree.... cautiously. Accepting that an initial, (sudden), wind force pushes the nose of the bullet with the wind until the gyroscopic forces react and nose up or down to precess into the wind, this exact motion seems to me would have the greatest pressure differential, (or lift effect), resulting in a "jump" of sorts relative to the value of a steady overturning moment caused by deceleration.

I roughly calculated a typical 6ppc bullets deceleration over 100 yards and compared the starting and ending values to a constant 13MPH crosswind. I got a change of about 1/10 of 1 percent in forward to side velocity ratio. I'm not sure my rough math value is important as I think it suggests the vector change would be very, very small. I agree it is there though.

I guess in part I'm thinking, in my experience, if all the flags are in the same direction, the changes in wind velocity doesn't seem to show up on the target as drastically as with a wind switch someplace. I'm reflecting back on some WTF moments right now.:D:eek:
 
Wilbur said:
You shouldn't hunt deer with a 22 short! Go with at least a long or long rifle....
Click to expand...

I've known members of the Nez Perce tribe who hunt elk with a 22 WMR. They shoot them behind the ear from smelling distance. (As to who smells whom first, I'm not sure, or if it matters.)
 
All of you who have this figured out, who really can explain how it works, tell me how it works when the projectile is a sphere, and there is no nose to point.
What would you think the magnitude (in degrees) of an elongated bullet's turning into or away from the wind depending on which you believe to be true) is, and how did you arrive at that number? Another question, what moves an empty tin can, laying on its side, on a horizontal surface, when the wind velocity is high enough for it to have an effect on the can's position, and its direction is at a right angle to the longitudinal axis of the cylinder? It seems to me that we often discuss the difference in our imaginings of what we cannot measure or observe directly, and refer to physics and math without furnishing any calculations as if the mere use of the words proved something. Finally, what do we mean when we say that something was blown by the wind, be it leaf or bullet?
 
Boyd Allen said:
All of you who have this figured out, who really can explain how it works, tell me how it works when the projectile is a sphere, and there is no nose to point.
What would you think the magnitude (in degrees) of an elongated bullet's turning into or away from the wind depending on which you believe to be true) is, and how did you arrive at that number? Another question, what moves an empty tin can, laying on its side, on a horizontal surface, when the wind velocity is high enough for it to have an effect on the can's position, and its direction is at a right angle to the longitudinal axis of the cylinder? It seems to me that we often discuss the difference in our imaginings of what we cannot measure or observe directly, and refer to physics and math without furnishing any calculations as if the mere use of the words proved something. Finally, what do we mean when we say that something was blown by the wind, be it leaf or bullet?
Click to expand...

Boyd,
I'm glad this thread isn't dead yet. If you want equations, they are not too difficult to find. McCoy has plenty that specifically apply to bullets, just make sure to check the errata. If you are more interested in a cylinder, then these lecture notes give the background on potential flow that leads to estimates of the Magnus effect: http://web.mit.edu/16.unified/www/FALL/fluids/Lectures/f16.pdf

The deflection angle for a 3000 fps bullet in a 10 mph (= 15 fps) wind? Turning into the wind requires a turn of arctan(15/3000) = 0.286 degrees.

How does air move a can, or a bullet for that matter? Great question, because the answer is the heart of fundamental fluid mechanics. Air (or any other fluid) can impart three forces to any point on a surface: 1) pressure, which is always perpendicular to the surface, and 2) two shear forces that are tangential to the surface and perpendicular to each other. These forces vary across the surface (of the can) and imbalances from one side to the other cause the can to accelerate: F = ma (Newton's law). The can will keep accelerating until all the forces are balanced.

Does a spinning sphere respond to a cross wind? Absolutely. Again, F=ma until F = 0, then a = 0. A cool video of a billiard ball suspended by a stream of air that demonstrates the effect that a cross wind can have: https://www.youtube.com/watch?v=LI9Mi1KhFTs&list=PL0EC6527BE871ABA3&index=6&feature=plpp_video
Sure, it isn't exactly the same situation as a musket ball in the wind, but it's motion is caused by the same three basic fluid forces. Whenever there is an imbalance in the forces, such as by a cross wind, the ball will respond. It has to.

Keith
 
Boyd Allen said:
All of you who have this figured out, who really can explain how it works, tell me how it works when the projectile is a sphere, and there is no nose to point.
What would you think the magnitude (in degrees) of an elongated bullet's turning into or away from the wind depending on which you believe to be true) is, and how did you arrive at that number? Another question, what moves an empty tin can, laying on its side, on a horizontal surface, when the wind velocity is high enough for it to have an effect on the can's position, and its direction is at a right angle to the longitudinal axis of the cylinder? It seems to me that we often discuss the difference in our imaginings of what we cannot measure or observe directly, and refer to physics and math without furnishing any calculations as if the mere use of the words proved something. Finally, what do we mean when we say that something was blown by the wind, be it leaf or bullet?
Click to expand...

Boyd - I certainly don't have this "figured out". I think I have a general understanding of the materials I was studying and as I said earlier, I am relying heavily on the work of others. Behind the scenes here, I've been talking with a forum member that feels rather passionately the materials I am relying on are flawed. I am in no position at this point to defend the math or disprove other theories.

Re: The sphere.

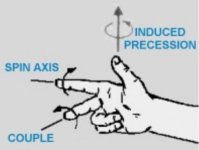
My understanding is a pointed bullet with a longitudinal axis , gyroscopically stable, will turn into the direction of airflow. This is stated as the overturning moment: http://www.nennstiel-ruprecht.de/bullfly/fig8.htm

Since a true sphere does not have a longitudinal axis, I can't see any reason why it would turn into the wind. A pointed bullet could not fly with its axis misaligned to the airflow or it would tumble. The gyroscopic forces cause the precession resulting in the realignment into the airflow. The gyroscopic forces on a sphere would try to keep its axis spinning in the same vector as it was launched. Unless a force is introduced to overcome the gyroscopic forces, it should stay as is.

A side wind force acts upon the center of pressure as stated here: http://www.nennstiel-ruprecht.de/bullfly/fig5.htm

A center of pressure will be present in a spherical bullet too. The wind is a force and the force is applied to the center of pressure resulting in drift. Specifically how it drifts and by what value I believe is very complex and is related to the following quote from the above site: "depends on the flowfield conditions". Or, related to the following quote from McCoy's book near the beginning of "Chapter 4: Notes on Aerodynamic Drag", citing:

"No attempt is made in this chapter to discuss the basic fluid dynamic and thermodynamic processes involved in the formation of boundary layers and shock waves. This book is about exterior ballistics, and space does not permit even a cursory review of the modern science of aerodynamics. References 9 through 12 are recommended to the reader who is interested in a more complete understanding of compressible flow, shock waves, and boundary layer theory."

Re: Your request for a magnitude (in degrees).

I believe this cannot be answered since bullet flight is so dynamic.

Re: The tin can.

The same thing that moves the same can if you stuck your finger on the side of it and gave it a push. More force on one side than the other.

Re: Finally, what do we mean when we say that something was blown by the wind, be it leaf or bullet?

Trying not to sound too sarcastic, but that would depend on who's saying it.:)

I'm not sure if any of this makes sense to you but I'm trying to leave my "imaginings" out of this. That's why I included the links.
 
Hmmmmm, Never thought about that

(QUOTE=Boyd Allen;746949]All of you who have this figured out, who really can explain how it works, tell me how it works when the projectile is a sphere, and there is no nose to point.
What would you think the magnitude (in degrees) of an elongated bullet's turning into or away from the wind depending on which you believe to be true) is, and how did you arrive at that number? Another question, what moves an empty tin can, laying on its side, on a horizontal surface, when the wind velocity is high enough for it to have an effect on the can's position, and its direction is at a right angle to the longitudinal axis of the cylinder? It seems to me that we often discuss the difference in our imaginings of what we cannot measure or observe directly, and refer to physics and math without furnishing any calculations as if the mere use of the words proved something. Finally, what do we mean when we say that something was blown by the wind, be it leaf or bullet?)



Oh man Boyd, I used up too many brain bytes trying to understand the difference between, "Come here" and "Go sic 'em." Maybe someone else can help. :) In the meantime, I'd like to tell you about a new acronym I learned from Alaninga, the originator of this thread. It's DMA. Yep, DMA stands for "Doesn't matter anyway." Isn't that great? :) The answer to anything, ",,,ah, well yeah, I don't know but DMA"

Later and best regards,

Gene Beggs
 
Well...

Harold Broughton told me early on that the bullet would "claw" it's way into the incoming airflow because it had higher pressure than on the opposite side of the bullet. Didn't matter how slick your bullet was...the rifling already ruined that. I mentioned that to Bo Clerke one time and his answer was simply "Harold ain't a stupid individual".
Bryan
 
My point about the round ball was that there had been a lot of discussion in a previous thread (some years ago) that seemed to indicate that lots of fellows were under the impression that a bullet's yaw in response to a cross wind was the CAUSE of wind drift. At the time, I brought up the round ball because it does not fit that model, and that therefore the model might be flawed. At the base of this is that the fact that if math, or physics are misapplied, then the end result of all of the impressive complication will be incorrect. At the root of this is that, in the absence of being able to directly measure the forces and observe small motions, we are in fact guessing. No one in that discussion could actually explain the references that they were under the impression that they fully understood. I know that this is a different group, but nevertheless, I think that there may be some common elements. Over all there was a general attitude of condescension expressed toward any who would use the simplified explanation that bullets are blown by the wind. This is why I asked the somewhat rhetorical question about what was meant by that. The whole thing about the offset between the center of mass and center of pressure causing the bullet to yaw, and that yaw causing drift seems to ignore several things. Center of pressure does not mean that the actual pressure is somehow magically applied to one point. It is applied against the whole profile of the bullet viewed from the angle of the cross wind, and this profile increases from a circle to a full side view as the angle of the crosswind changes from zero to 90 degrees. With a constant pressure per square inch, a larger area equals more applied force, and deflection. Of course it is the pressure the imbalance of forces that moves anything, but it seems silly to say that that the wind does not blow bullets. They are displaced laterally by forces that originate from the existence of some degree of cross wind. To me that is being blown. Finally, formulas that are not perfect predictors of what happens in the real world may be very useful, despite their imperfections, ballistic coefficients being an example. Just because a better model has been developed does not mean that the old one was not useful.
 
You must log in or register to reply here.
Back
Top